A Spread Trade for IEF

DRAFT

Paul Teetor

Summary

The iShares Barclays 7-10 Year Treasury Bond Fund (NYSE: IEF), is an exchange-traded fund which holds primarily intermediate-term US Treasury Notes. As the name suggests, the maturities of the holdings range from 7 to 10 years.

I wanted to determine if IEF could be hedged or replicated using a combination of Treasury futures. If so, it might be possible to trade the spread between IEF and futures. I initially modeled the hedge/spread using Eurodollar, 2-year, 5-year, and 10-years futures.

The final model, however, required only the 10-year futures. Furthermore, the model residuals are demonstrably mean-reverting, which naturally leads to relative value trades. This is very encouraging because it suggests a simple spread -- IEF versus 10-year Treasury Note futures -- could be profitably traded.

Model Development

Full Model

The initial, full model was a time-series regression on the futures prices using daily closing prices.

IEF_i = β₀ + β_ED×ED_i + β_TU×TU_i + β_FV×FV_i + β_TY×TY_i + ε_i

ε_i ~ ARIMA(p, 1, q)

where

ED is Eurodollar futures
TU is the 2-year Treasury note futures
FV is the 5-year Treasury note futures, and
TY is the 10-year Treasury note futures.

The initial fit selected p = 3 and q = 4, giving an ARIMA(3,1,4) model for the residuals.

I assumed that the FV and TY futures would be necessary for modeling IEF since the futures would, essentially, create a bar-bell portfolio which matched the average maturity of the bond fund. I included ED in case the ETF, which pays monthly dividends, was sensitive to short-term rate movements. I included TU simply for completeness, without expectation it would be a significant predictor.

Reduced Model

The TU proved to be insignificant, which was not surprising. The ED term was also insignificant, which was reasonable but a little surprising.

I was quite surprised, however, that the FV term was also insignificant. Evidently, the 10-year futures, TY, is sufficient to mimic the fund behaviour without the 5-year bar-bell component. The final, reduced model was very simple:

IEF_i = β₀ + β_TY×TY_i + ε_i

ε_i ~ ARIMA(p, 1, q)

A re-fit of the ARIMA model gave p = 1 and q = 2, for a final ARIMA(1,1,2) model of ε. The indicated hedge ratio was approximately 1,308 shares of IEF for each TY contract.

Model Assessment

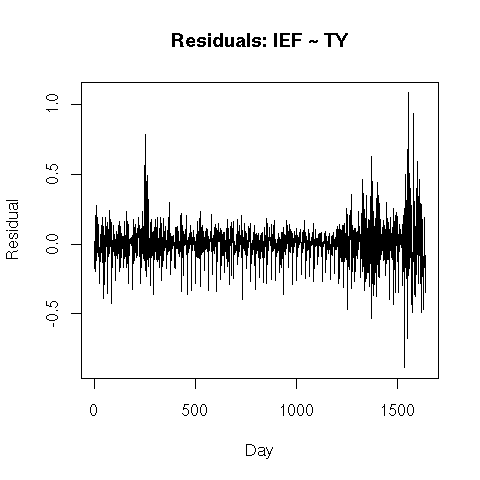
The model residuals are mostly clean and show no bias.

An obvious problem is the explosion in variance in the recent residuals (extreme right-hand side). I assume this is caused by the unprecedented conditions during the financial markets' melt-down of 2008. From a modeling standpoint, it suggests that the market has entered a new regime, and the model may require a local re-fit.

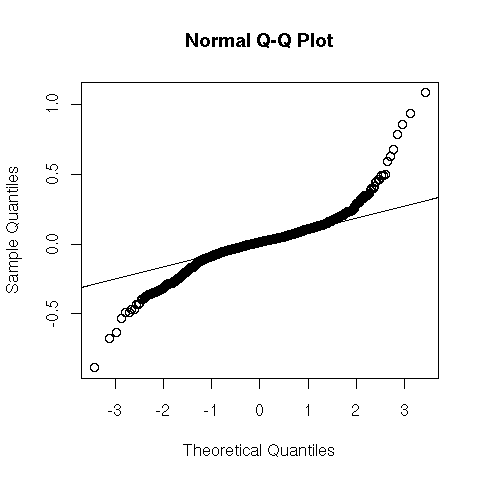
The variance explosion is echoed in the Normal quantile-quantile plot of the residuals.

Clearly, there are out-sized residuals, as indicated by the fat tails. This casts some suspicion on the model, but might be explained by the excessive market volatility of 2008.

Testing the residuals for mean reversion gives a p-value of essentially zero, using the Augmented Dickey-Fuller test, so we can be confident they are mean-reverting. This is no surprise after seeing the plot of residuals, above.

Conclusions

The main result here is that the 10-year Treasury Note futures (TY) seem sufficient for hedging the IEF stock. This is a welcome result because the spread trade is quite simple and does not require a basket of futures contracts.

A second result is that the model's residuals are historically mean reverting, creating the opportunity for mean-reversion trades: the residuals act as indicators of over- and under-valuation, letting us enter the spread at opportune times. This chart of recent residuals illustrates some typical opportunities.

Notice that the mispricing strayed from zero, but reliably returned to the mean. The extremes of those deviations represented trading opportunities.

Limitations

This is only a preliminary study. A deeper study could address these issues, among others.

The study used closing prices, which are dissynchronized between the futures market (3:00 PM Eastern) and the stock market (4:00 PM Eastern). The unmatched closing times inevitably introduce unwelcome noise into the model.
The recent large variance in the residuals needs further research. Will a simple re-fit of the model to recent data eliminate the excess variance, including the fat tails in the Q-Q diagram?
This study used Perpetual Data® from Commodity Systems Inc. for futures prices. This is convenient for a quick study, but should probably be replaced by roll-forward data in order to improve the model's credibility.

Acknowledgments

I am grateful to Art Margulis of Cognitive Capital for suggesting the idea of trading some ETFs as if they are fixed-income instruments. I am also grateful to Mohamed Amezziane of DePaul University for his constructive comments on fitting the model.